- Đăng Ký
- Đăng Nhập
- Mở Shop

Bài 9: Tính chất ba đường cao của tam giác thuộc Giải Toán 7
Bài 58 (trang 83 SGK Toán 7 tập 2): Hãy giải thích tại sao trực tâm của tam giác vuông trùng với đỉnh góc vuông và trực tâm của tam giác tù nằm ở bên ngoài tam giác.
Lời giải:
+ Xét ΔABC vuông tại A
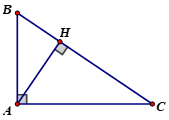
AB ⏊AC ⇒ AB là đường cao ứng với cạnh AC và AC là đường cao ứng với cạnh AB
hay AB, AC là hai đường cao của tam giác ABC.
Mà AB cắt AC tại A
⇒ A là trực tâm của tam giác vuông ABC.
Vậy: trực tâm của tam giác vuông trùng với đỉnh góc vuông
+ Xét ΔABC tù có góc A tù, các đường cao CE, BF (E thuộc AB, F thuộc AC), trực tâm H.
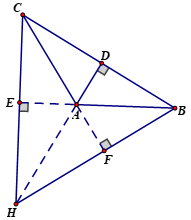
+ Giả sử E nằm giữa A và B, khi đó
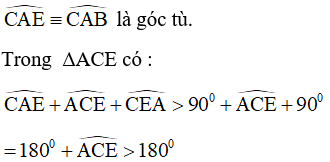
Vậy E nằm ngoài A và B
⇒ tia CE nằm ngoài tia CA và tia CB ⇒ tia CE nằm bên ngoài ΔABC.
+ Tương tự ta có tia BF nằm bên ngoài ΔABC.
+ Trực tâm H là giao của BF và CE ⇒ H nằm bên ngoài ΔABC.
Vậy : trực tâm của tam giác tù nằm ở bên ngoài tam giác.
Kiến thức áp dụng
+ Ba đường cao trong tam giác đồng quy tại một điểm. Do đó khi xác định trực tâm ta chỉ cần xác định giao của hai đường cao.
+ Định lý tổng ba góc trong một tam giác : Trong một tam giác, tổng ba góc bằng 180o.
Chú ý: CongMuaBan.vn không bán hàng trực tiếp, quý khách mua hàng xin vui lòng liên lạc với người bán.